The Chessboard High Five Problem
A Probability Brain Teaser. If you love solving puzzles you will definitely enjoy this challenge.
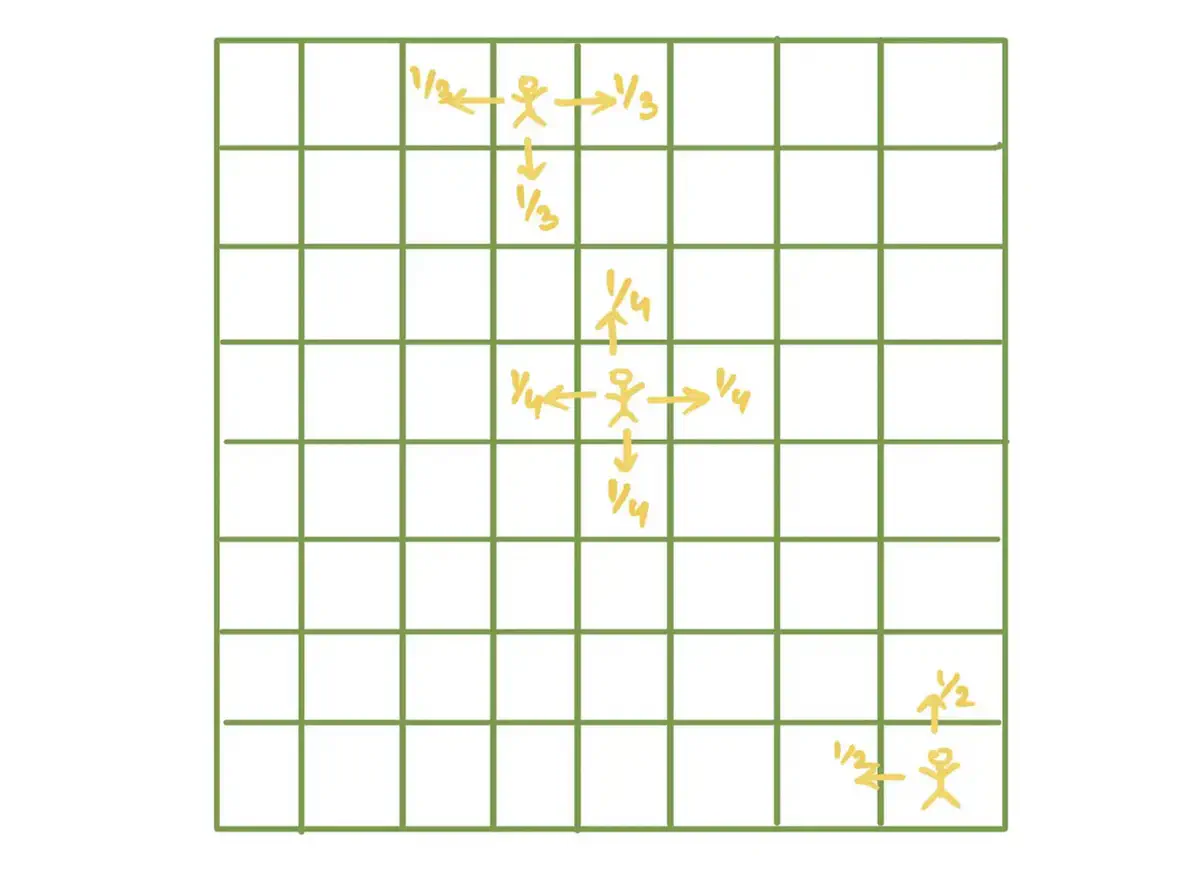 Image credit: Me
Image credit: Me
Just another day, when I was browsing through my Instagram feed, my friend sent me this interesting yet not so difficult problem involving understanding of basic probability, counting and bit of time to pause the temptation to scroll the rest of your Instagram feed.
So, the problem went like this..
Imagine you have a regular 8 x 8 chessboard, with 64 people standing on each of the 64 squares. At the same time every person turns to face one of their neighbors with equal chances i.e. say the person near the center of the chessboard can face any direction with 1/4 probability, a person at the top of the chessboard (but not the corners) has probability 1/3 to face any of its neighbors, similarly all others. Now, if two people are facing each other they give each other a high five. Find the expected number of high fives.
Read my detailed solution at: The Chessboard High Five Problem